Barry's Coilguns
AC Linear Induction Motor
- Introduction
- Experiment
- Line-Throwing Gun
- Thrust
- Thrust Constant
- Losses
- Traveling Waves
- Resistance
- Capacitors
- Series Parallel
- Energy Storage
- Power Shifting
- Projectile Heat
- Magnetic Field
- Impedance Drop
- About Northrup
- Preface
Use of the Thrust Constant
in the Design of the Coil Gun
From the narrative, the length of the gun is taken as 1000 meters, the inside diameter as 40.0 centimeters, and the outside diameter of the projectile as 37.0 centimeters, the length of the projectile exclusive of nose and tailpiece being 500 centimeters. Selecting a thrust constant of 13 x 10-6 grams, we find from experimental data that the following coil and cylinder proportions must exist:
- The phase difference between unit coils must be sixty electrical degrees.
- The physical coupling, or the relative cross-sectional area of the projectile and the inside of the coil, must be about 86%.
- The length of the magnetic travelling wave must be about 2.6 times the inside diameter of the coil. Six unit coils, sixty electrical degrees apart, constitute three hundred and sixty degrees or one complete cycle, or in this case one wave. The wave-length is thus six times the distance between centers of adjacent phase coils.
- For maximum thrust, the effective a.c. resistance and the reactance of the induced current paths in the projectile must be equal.
From the foregoing proportions, together with other data, we arrive at the following specifications for the one-kilometer-long electric gun:
- Length of gun = 1000 meters 40.0 cms.
- Inside diameter of gun = 40.0 cms.
- Outside diameter of copper conductor tubing = 1.0 cms.
- Wall thickness of tubing = 0.34 cms.
- Number of phase coils = 5880
- Length of phase coils = 14.4 cms
- Space between phase coils = 2.6 cms
- Wave-length = 102 cms
- Turns per phase coil =12
- Mean length of copper tubing in phase coil = 15.5 cms
- Frequency = 2000 cycles
- Wave speed = 2040 m. per sec.
- A.c. resistance of one phase coil at approximately 15 x 10-4 ohm per meter = 0.023 ohm
- Approximate inductance of phase coil = 0.000007 henry
- Approximate empty reactance at 2000 cycles = 0.88 ohm
- Approximate weight of projectile = 100 kilograms
- Average turns per centimeter, taken over wave-length of 102 centimeters = 0.705
From the equations given under the General Laws of Motion it is shown that the acceleration of a projectile in the gun is expressed by the formula:
![]()
where a is the average acceleration due to magnetic thrust, v the muzzle velocity in meters per second, and l the length of the gun in meters. For the projectile to attain a muzzle velocity of 1000 meters per second in a gun 1000 meters long we have:
![]()
From the same general equations it can be shown that the force in kilograms necessary to impart an acceleration of 500 meters persecond per second to a projectile is given as:
![]()
where T is the thrust in kilograms, w the weight of the projectile in the same units, a the acceleration of the projectile in the gun, in meters per second per second, and g the acceleration of gravity. Substituting numerical values in (2):
![]()
When the gun is in a vertical position, an additional thrust must be exerted to balance the weight of the projectile, besides the thrust necessary to give vertical speed. Formula (2) is then modified as follows:
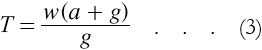
The corrected value for T by (3) is:
![]()
Having determined the total thrust necessary to give the desired acceleration and velocity, we approach the problem of obtaining this thrust with polyphase magnetic waves.
As shown in the previous section, the magnetizing force inampere turns per centimeter is given by the formula
![]()
where T is the total thrust on the projectile in grams, K the thrust constant, A the area of the projectile on which the thrust is effective, in square centimeters, and the product (in) is equal to the ampere turns per centimeter.
From (3) we have found the total thrust to be 5200 kilograms or 5.2 x 106 grams; the maximum value of K has been found by experiment to be 13 x 10-6 gram; the active area of the projectile is taken as the area of a cylinder 500 centimeters long and 37 centimeters in diameter, which calculates out as approximately 58,200 square centimeters. Thus, by (4),
![]()
As there is only an average value of 0.705 turn per centimeter length of the gun, the current per phase necessary to produce 2620 ampere turns (found by dividing the average number of turns per centimeter of length into the required ampere turns) is 3720 amperes.
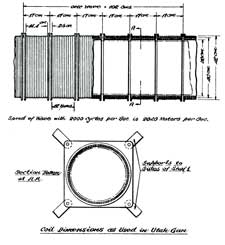
Figure 1. Coil dimensions used in the Utah gun
As mentioned elsewhere, the maximum thrust constant cannot be realized except under certain set conditions, the main condition being that the frequency of the currents induced in the cylindrical shell of the projectile shall be such as to make the electrical resistance and the reactance of the induced current paths substantially equal.
Under the influence of the travelling magnetic wave produced in the electric gun, the projectile is started from rest and gains speed. In general, the velocity of the magnetic wave remains constant, whereas the speed of the projectile varies from zero to a theoretical value known as the synchronous speed, which is the same as the speed of the wave.
In practice, the projectile speed is less than synchronous speed by an amount known as the “slip.” The slip is the difference between the speed of the projectile and the synchronous speed, and is given in terms of percentage of synchronous speed. Thus, one hundred per cent slip means that the projectile is at a standstill; fifty per cent slip indicates half of synchronous speed; while at zero slip the projectile is the same velocity as the wave.
It is possible to show that the frequency of the currents induced in the projectile is a direct function of the slip. This means that the relation of resistance to reactance constantly changes as the projectile gains velocity — which in turn affects the value of the thrust constant K. By suitable design of the projectile the maximum thrust constant can be made to come at any convenient value of slip.
Certain experimental and theoretical considerations show that if the maximum or muzzle velocity of the projectile is equal to a fifty per cent slip, and the resistance and reactance factors are balanced to give the maximum thrust constant with this slip, then the thrust constant will not decrease more than twenty per cent under stationary conditions. Hence, in starting the projectile, the thrust constant will not be less than eighty per cent of the maximum value which will occur at maximum velocity.
By (4), the ampere turns per centimeter necessary to maintain a constant total thrust varies as the inverse square root of the value at K. Hence, with K at eighty per cent of its maximum value the impere turns will be increased by a factor of one over the square root of eight-tenths, or 1.12. The current per phase at the start should then be about twelve per cent higher than the value calculated with the rise of the maximum value of K. The starting current per phase is thus about 4170 amperes.
| < Previous | Page 5 of 17 | Next > |
©1998-2026 Barry Hansen