Barry's Coilguns
Coilgun Mark 2
- Introduction
- Hints and Suggestions
- RLC Simulation
- RLC Analysis
- LC Time Sim
- Inductor Sim
- Wire Loop
- Java
- Photographs
- Schematic
- SCR
- Construction
- Result: Position
- Result: Turns
- Result: Length
- Result: Iron
- Result: Tube
- Result: Voltage
Wire Loop Equations
This page describes equations to model the simplest possible solenoid - a single wire formed into a loop. It selects a few points of interest to help understand the magnetic field. A Java applet will be written to graphically illustrate this magnetic field -- please check back each week so you can play with it when it's ready.
When the Java applet is completed, you should see a graph (below) with slider controls to adjust the size of the loop. The graph shows you the magnetic field intensity along the main axis, and the force on a particle. To keep the controls very simple, we have normalized all curves so they peak at a value of 1.0. The only thing you can adjust is the loop's radius.
Magnetic Field Strength
The magnetic field has been normalized to the peak field. That is, the graph shows the ratio of Bz to Bz=0. To see how the equations are derived, please visit theory of wire loops.
The normalized B-field is given by the equation:
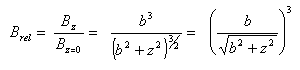
- b = radius of loop
- z = point of interest along z-axis
- Brel = ratio of B-field at this point, compared to the maximum B-field
That was very nice, but what if you want to know the point z for a particular Brel?
Solve the above equation for z in terms of Brel, and you get:
![]()
Force on a Particle
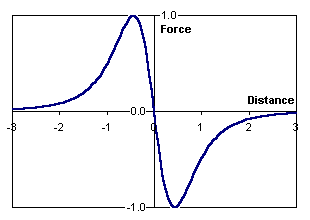
Now let's introduce a tiny particle, one small enough that the shape of the B-field is not disturbed. The force on this small particle is the derivative of the B-field squared. The normalized force equation plotted above is:

Observations
 This equation maintains the same general shape for various
sizes of a radius. It is merely scaled up or down according to its radius. You can see how quickly
the field falls off as you move away from the center of the loop.
This equation maintains the same general shape for various
sizes of a radius. It is merely scaled up or down according to its radius. You can see how quickly
the field falls off as you move away from the center of the loop.
The force on a tiny particle in this magnetic field is shown in the simulator above. It is proportional to the gradient of the B-field squared.
You can see the force is positive on the left, negative on the right, and zero at the center of the wire loop. The sign (+ or -) shows the tendency to pull a projectile from either side back into the middle.
We kept this applet as simple as possible. It would be nice to find the exit speed of a particle in this field, but that would require factors such as starting position, current over time, mass and permeability. (Maybe later!)
Some Selected Points
The B-field equation can be solved for a few selected points using algebra. It would be interesting to know the field strength at one radius away from the center, and where the field is one-half peak value, and where the field is negligible.
At exactly one radius from the center, the point z is equal to the radius b. Substituting this
value of z, and solving for B:
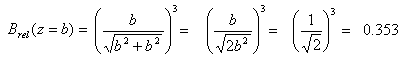
If we want to find point z for a certain value of Brel, we use algebra to reverse the equation:
When the field is one-half of the peak value, Brel = 0.5. Substituting this value for Brel and evaluating z:
z = b*0.7664 when Brel = 1/2
This result is very interesting! It says the magnetic field is practically gone at a distance of about twice the radius from the midpoint of the loop! And we know that 'twice the radius' is another name for its diameter. An old rule-of-thumb has said exactly this, and now we know the analytical reasoning behind it.
One last point... let's find where the field disappears. The field strength can be assumed negligible when it is reduced to less than 10% of the peak value. So let's solve for z when Brel = 0.1. Beyond this distance we can simply ignore the B-field:
z = b*1.908 when Brel = 1/10
| < Previous | Page 7 of 18 | Next > |
©1998-2026 Barry Hansen