Practical Coilgun Design
Magnetic Materials
- Magnetic Materials
- Solenoid Physics
- Magnetic Field
- Force From Magnetism
- Saturation
- Saliency Ratio
- Salient Pole Motors
- Electromagnetic Guns
- Widescreen LCD
- IEEE Articles
- Bibliography
Saturation
Is there a limit to magnetic field strength? What happens to the projectile when the coil is boosted to an extremely strong magnetic field?
Are you familiar with B-H curves? First, a quick refresher about the definitions of B and H.
- The magnetic field, H, tends to magnetize space.
- The magnetic flux density, B, is the total magnetic effect that results.
The two concepts are approximately linked with a simple equation. The magnetic flux density, B, is the total magnetic effect that results in iron: B = u0 * ur * H, where u0 is the permeability of free space, and ur is the relative permeability of the material.
The constant ur is essentially unity (= 1.0) for all materials except ferromagnetic materials, notably iron, for which the value of the relative permeability lies typically in the range 1000 to 10,000. Thus for iron, a small magnetic cause, H, creates a large magnetic effect, B.
By the way, an iron/nickel compound typically has twice the constant relative permeability (ur) as mere iron. The highest ur is "Supermalloy" at about 100,000 (see table of magnetic materials) So you might think it would perform much better than a plain iron projectile. Unfortunately, it ain't necessarily so. The total flux in a magnetic circuit is limited by any air gaps, and we've got a big one: right down the middle of the coil.
 But
a more complete picture takes into account saturation. As the applied field increases, more and
more magnetic domains within the ferrous material will align themselves with the external field.
This temporarily makes the core act as a magnet itself, which for us will improve the forces
upon the projectile. At small to medium applied fields, the flux density B is nearly linear with
respect to the applied field H. But at very strong applied fields, almost all the magnetic domains
are aligned.
But
a more complete picture takes into account saturation. As the applied field increases, more and
more magnetic domains within the ferrous material will align themselves with the external field.
This temporarily makes the core act as a magnet itself, which for us will improve the forces
upon the projectile. At small to medium applied fields, the flux density B is nearly linear with
respect to the applied field H. But at very strong applied fields, almost all the magnetic domains
are aligned.
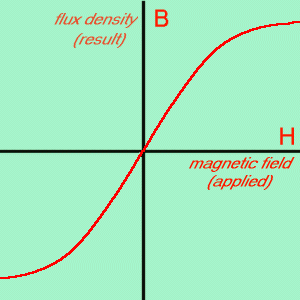
The B-H curve here illustrates the effect of magnetic saturation. It shows the effect of applying an external magnetic field to unmagnetized iron. The magnetism curve starts at the origin (0,0) and increases linearly as the magnetic field magnetizes the iron. The slope of the curve in this region is u = u0 ur. Eventually, however, all the magnetic domains align with the applied field, and the curve flattens out as the iron becomes magnetically saturated. As we reverse the applied magnetic field, the iron eventually becomes magnetized in the reverse direction until it again saturates.
How does this relate to our projectiles? It means measurements of forces taken at small coil currents are linear with respect to applied current. As you increase current, the magnetizing force produced by an air coil is always linear, but the response in the projectile is not linear. At very large fields, the force in the projectile is not as great as linear equations would lead you to expect. The mechanical force of attraction does continue to increase, but it takes more and more coil current to achieve the same amount of increase.
Conclusion
So how do you apply that general concept to a physical system? The magnetic saturation point puts a limit on the maximum effective strength to drive your coil. There will be no benefit at all if you exceed this, only wasted heat.
Basically it goes like this. You need to know the exact material and dimensions of your projectile. From that, manufacturers supply the ferromagnetic permeability (or see the table of magnetic materials) and the B-H curve. From the saturation point, Bs, you know the upper limit for your design; it would be wasteful to attempt any higher flux density.
You also need to compute the total reluctance R along the path of your magnetic circuit. From Bs and R you can compute the maximum flux your coil should generate. But don't worry: this upper limit is going to be huge! My initial calculation found it will be millions of ampere-turns, using any air-core coil that we've seen so far!
| < Previous | Page 5 of 11 | Next > |
©1998-2026 Barry Hansen