Barry's Coilguns
Coilgun Mark 2
- Introduction
- Hints and Suggestions
- RLC Simulation
- RLC Analysis
- LC Time Sim
- Inductor Sim
- Wire Loop
- Java
- Photographs
- Schematic
- SCR
- Construction
- Result: Position
- Result: Turns
- Result: Length
- Result: Iron
- Result: Tube
- Result: Voltage
Mark II Results, 23v
This page provides coilgun measurements and analysis of performance.
The Mark II coilgun design (remember, goal is minimum parts count) fires at 7.8 m/s with:
- the projectile is 44.7 mm in length and 6.0 mm diameter, weighing 10.03 g.
- the coil is 40 mm long, wound with four layers of 18 AWG magnet wire in 30 turns per layer, with no external iron.
- the capacitor is 24,000 uF, and is charged to 55 volts for a total of 36.3 J.
By the way, 7 m/s is equivalent to a flight of eight feet out and two feet down. Not much danger to anyone... except maybe my own feet!
Projectile's Starting Position
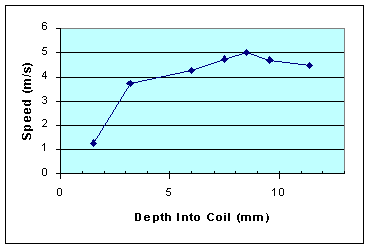 The
exit speed is quite sensitive to the projectile's precise starting position. It takes only a
few millimeters further in or out to gain or loose significant speed. This graph shows the measured
speed compared to how far the projectile was inserted into the coil.
The
exit speed is quite sensitive to the projectile's precise starting position. It takes only a
few millimeters further in or out to gain or loose significant speed. This graph shows the measured
speed compared to how far the projectile was inserted into the coil.
| Depth | Speed |
|---|---|
| 18.6 mm | 4.46 m/s |
| 20.4 | 4.67 |
| 21.5 | 5.00 |
| 22.5 | 4.73 |
| 24.0 | 4.26 |
| 26.8 | 3.73 |
| 28.5 | 1.25 |
Conclusion - A projectile's starting position must tuned to be within a 2mm range to achieve optimum results.
Number of Turns in Coil
The timing is entirely controlled by the inductance and capacitance. The coil should be wound with taps at various layers, so you can choose the number of turns and therefore the inductance. This is crucial to the success of the Mark II coilgun! The graph at right shows the exit speed according to the number of layers I used.
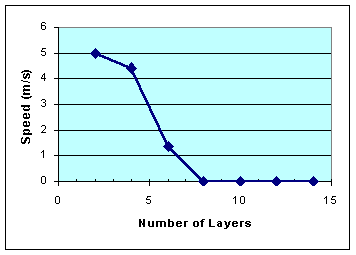
| Layers | Result |
|---|---|
| 14 | strong snap to stay in middle of coil |
| 12 | strong snap to stay in middle of coil |
| 10 | strong snap to stay in middle of coil |
| 8 | strong snap then fell out wrong end of barre |
| 6 | 1.39 m/s forward |
| 4 | 4.41 m/s |
| 2 | 5.00 m/s |
My coil brought out a tap at every other layer. Tuning the coilgun involved connecting the power to various taps and firing it. Too much inductance means the magnetic field stays on too long, and the projectile is held in the middle of the coil. Too little inductance means the magnetism is on too short, and the projectile may barely move.
Conclusion - My coil had fourteen layers, but the best results occurred using only the first two layers. (If I had known that, I could have saved a lot of winding!) My next coil should be designed with lower inductance, and have more taps for more choices. Note that inductance is proportional to the square of the number of turns.
Length of Projectile
The projectile length affects performance, but how?. Shorter projectiles have greater acceleration for the same force, but they also have less material to interact with the magnetic field. And if they do go faster, do they carry more or less kinetic energy than longer projectiles?
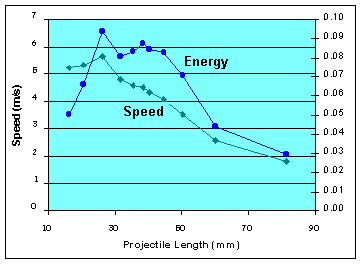 I
measured the performance of projectiles of eleven different lengths, ranging from 15mm to 80mm.
I calculated the average muzzle velocity and kinetic energy (Joules) for each projectile, shown
on the graph at right.
I
measured the performance of projectiles of eleven different lengths, ranging from 15mm to 80mm.
I calculated the average muzzle velocity and kinetic energy (Joules) for each projectile, shown
on the graph at right.
Length Speed Energy
16.3 5.24 0.0501
20.6 5.34 0.0659
26.2 5.64 0.0936
31.5 4.78 0.0808
35.4 4.58 0.0832
38.4 4.51 0.0875
40.3 4.32 0.0845
44.7 4.07 0.0831
50.3 3.53 0.0704
60.0 2.56 0.0442
81.3 1.80 0.0295
It is important to adjust the starting position for each projectile. As discovered in the tests above, the exit speed is rather sensitive to the particular starting position. There is a range of 6mm which permits operation, and an ideal range of only 2mm of variation in initial placement. Since the difference between projectiles was generally 5mm, some adjustment is needed for each one. I arranged it so the front of each projectile was inserted the same (ideal) amount into the coil. This gave quite satisfactory results, saving the effort of re-discovering the optimum starting position for each test.
My testing made at least five measurements from each projectile and averaged the results. Note there was often a 10% speed variation between shots using an identical setup. It would be instructive to analyze the variance, but that was more work than I cared to do.
Conclusions - Shorter projectiles went faster than longer ones. The fastest projectile was 26mm long, and it flew at 5.6 m/s.
There is what might be a linear relation between speed and projectile length, of roughly v = (-0.0688)x + 7.096, where v is m/s and x is length in mm. This seems to hold for projectiles in the range -25% to +50% of the coil length. The data could also match an inverse relationship (which would be consistent with a constant energy transfer), but the data is not smooth enough to be conclusive.
The energy curve is interesting. The kinetic energy stored in the projectile forms a hump which is within 10% of flat for projectiles in the range -25% to +25% of the coil length. There seems to be a constant energy transfer for projectiles nearly the same length as the coil. If not exactly constant, it is enough to conclude coilguns are not sensitive to projectile length over this small range.
External Iron
This coilgun was built with iron washers at each end to help focus the magnetic field. Did it really help?
I measured the performance, both with and without the external iron parts around the coil, using the same 31.5mm projectile and applied 24.3 volts. Because this might make a large change in inductance, the coilgun was tuned for both number of turns and starting position to reach best performance in each case.
With Iron Without Iron
4.78 m/s 5.93 m/s
In running this test, I discovered the "no iron" version worked best using four layers of the coil, compared to using two layers when external iron is there. This tells us iron ;makes a big difference to the inductance!
Conclusions - This coilgun works best with no external iron.
Capacitor Voltage
What is the relationship between muzzle speed versus capacitor voltage?
I measured speed at various applied voltages, and plotted the results below. The test was repeated with another projectile which was 50% longer than the first. Using significantly different lengths will tell us more about this dependence.
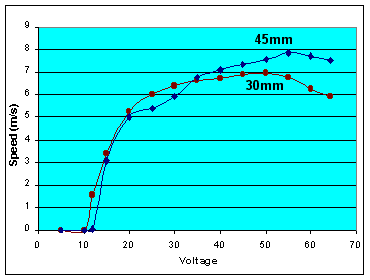
| Volts |
30mm Speed |
45mm Speed |
|---|---|---|
| 5v | 0 | 0 |
| 10v | 0 | 0 |
| 12v | 1.56 m/s | 0.07 m/s |
| 15v | 3.40 | 3.06 |
| 20v | 5.24 | 5.00 |
| 25v | 6.01 | 5.42 |
| 30v | 6.40 | 5.90 |
| 35v | 6.61 | 6.80 |
| 40v | 6.74 | 7.09 |
| 45v | 6.91 | 7.34 |
| 50v | 6.96 | 7.60 |
| 55v | 6.75 | 7.85 |
| 60v | 6.26 | 7.71 |
| 64v | 5.91 | 7.51 |
A minimum voltage of 10v was required to make the coilgun work at all. At low voltages (10 to 30v) the speed is extremely sensitive to voltage. The shape of the curve suggests a parabola, i.e. Speed = K*SQRT(volts - 10). At medium voltages (30 to 60v) the speed is fairly flat, and varies about 10% with respect to voltage.
At higher voltages (60+ volts) the speed drops off. The gun sounded a little distressed, as it made definite thumping noises during firing. I believe this is because at higher speeds the projectile is trying to leave the coil before the magnetic field has died, and it decelerates before it is gone.
There is a curious dip in the 45mm curve from 20v to 30v. I have no explanation for it. It would appear to be a measurement error, but I repeated the testing over this range and got the same results.
The longer projectile went 12% faster than the shorter one. This suggests an even longer projectile may go a little faster yet. The effect is not large; notice that one projectile was 50% longer than the other.
Conclusions - A key lesson is how to tune the coilgun with voltage. Notice the sharp knee around 20 to 30 volts. Then only 10% gain is achieved when the voltage is doubled to 60 volts. A reasonable tuning strategy is to gradually increase the voltage until this knee is identified. Further voltage increases will stress the circuitry without providing significant benefits.
Energy Conversion Efficiency
Out of curiosity, I also calculated the machine's efficiency at each voltage, as a ratio of kinetic energy (1/2 m v2) to stored energy (1/2 C V2).
| Volts |
30mm Efficiency |
45mm Efficiency |
|---|---|---|
| 12v | 0.5% | 0.0% |
| 15v | 1.5% | 1.8% |
| 20v | 2.0% | 2.7% |
| 25v | 1.7% | 2.0% |
| 30v | 1.3% | 1.7% |
| 35v | 1.1% | 1.6% |
| 40v | 0.8% | 1.3% |
| 45v | 0.7% | 1.1% |
| 50v | 0.6% | 1.0% |
| 55v | 0.4% | 0.9% |
| 60v | 0.3% | 0.7% |
| 64v | 0.2% | 0.6% |
This model is up to 2.7% efficient in converting stored energy into kinetic energy. Frankly, this is rather higher than I expected.
The capacitors store 4.8 joules at 20vdc. The 31.5mm projectile weighs 7.07 grams, and the 44.7mm projectile weighs 10.07 grams. The kinetic energy is computed from E = 0.5 m v^2, so the approximate energy at 5.24 m/s is 0.0971 joules. The energy conversion efficiency is Eout/Ein.
Conclusions - The important point here is to use the efficiency figure to design the next coilgun. Assuming the next model (or a higher voltage) is this efficient, you can work backwards to estimate the exit speed. From the speed, you can estimate the timing needed for the coil. And from the timing, you can compute the necessary inductance for a given storage capacitor. Neat, eh?!
| < Previous | Page n of 18 | Next > |
©1998-2025 Barry Hansen