FEMM - Magnetic Gun Club

This page reproduced from the Internet Archives WayBack Machine, 27 May 2003.

The Magnetic Gun Club once had this valuable page, which has since gone offline.
Original: web2.airmail.net/jd4usa/guncoil5.htm, and mgc314.home.attbi.com

Coil Analysis 1

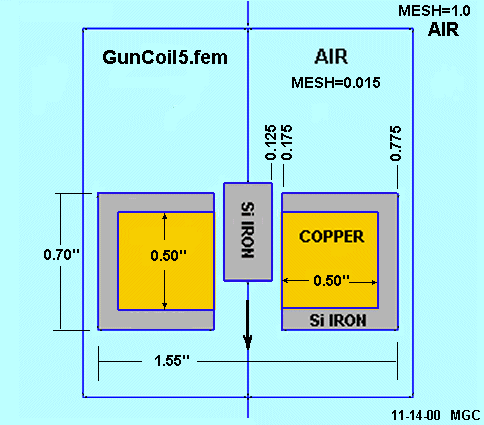
We'll begin our design by examining the magnetic properties of a coil configuration that might be useful for a coil gun. This figure shows a coil with a magnetic shield around it. The metal shield and the projectile are silicon iron (a standard material in the FEMM library). The projectile is 0.5 inches long and weighs about 3 grams. It travels along the vertical axis from top to bottom. Although FEMM only requires that the right half of the diagram be entered as data, this is a more illustrative picture of a crossection of the complete coil.

Two different air regions are used in order to get better resolution near the coil. The outer air region is much larger and includes the weaker flux some distance from the coil. Dimensions are in inches.

The coil itself is not modeled as individual turns of wire, but rather as a solid copper conducter with a specified current density. In the final construction, the number of turns of wire per unit area will be used to calculate the actual current that flows into the coil. For example, if the current density is 1000 amps/sq_mm and the wire that we use for the coil has an area of 10 sq_mm then the current would be 100 amps. (It's the product of amps * turns that matters).

Later we'll see how the wire size also affects the inductance and hence our switching circuits, but for now we'll just think of the coil as having a single turn with a very large current. The magnetic field is assumed static (not changing) so the inductance doesn't affect the force calculation. This is a simplification of the real case where the actual field is a function of time as the current changes and the projectile travels through the barrel. Nevertheless, this will give us a rough idea of the coil capability before we commit resources to building hardware.

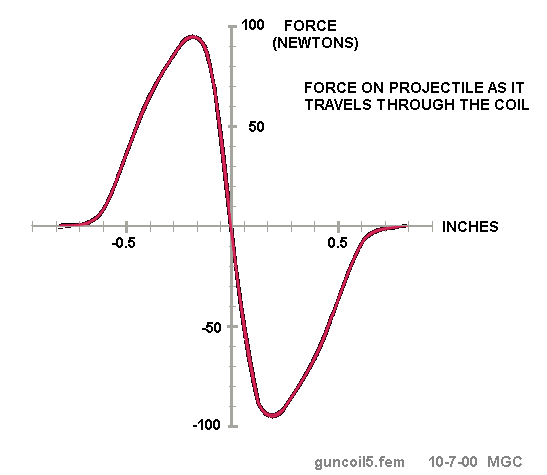This figure shows the force on the projectile as it moves along the axis. Distance is measured between the center of the projectile and the center of the coil. Because of symmetry, the force is zero when the projectile is at the center of the coil. As it moves out of the coil, the force changes sign and acts to pull the projectile back.

(1 Newton = 0.2248 pounds)

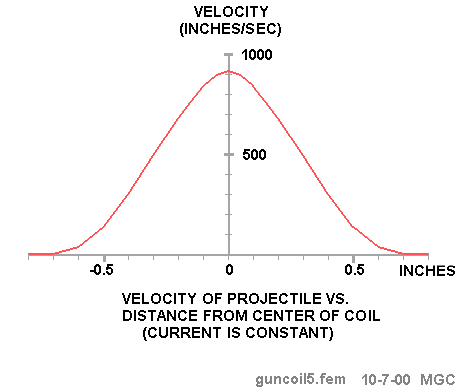The energy delivered to the projectile is equal to the integral of force times the distance, so we can find the kinetic energy of the projectile as any point and from that, its velocity. This curve was calculated by integrating the force curve from -infinity to X to find the total amount of work done on the projectile by the magnetic field. The velocity was then found using:

Energy=0.5*mass*velocity^2

The mass of the projectile is 3 grams. The velocity reaches its peak when the projectile is at the center of the coil. If the current is left on (and remains constant), the velocity will be zero when the coil reaches the other side of the coil. To avoid this retarding effect, the coil current has to be reduced to a low value as quickly as possible after the projectile reaches the center of the coil.

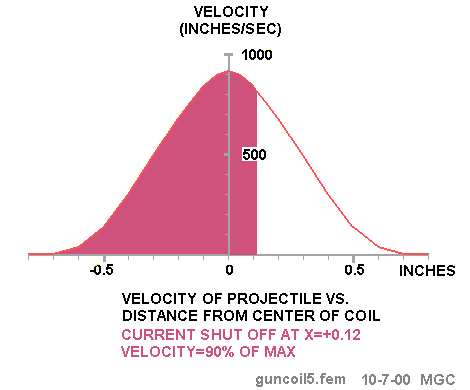This figure shows that by shutting off the current by the time the projectile reaches X=0.12, we can retain 90% of the peak velocity. Of course, shutting off the current exactly at X=0 would be ideal but there are some limitations in the switching circuit that compromise this ideal strategy. The problem is that the magnetic field has stored energy and this energy has to be dissipated or otherwise removed and this takes time. Since the projectile is travelling about 900 inches per second, it only takes 133 microseconds for it to travel 0.12 inch.

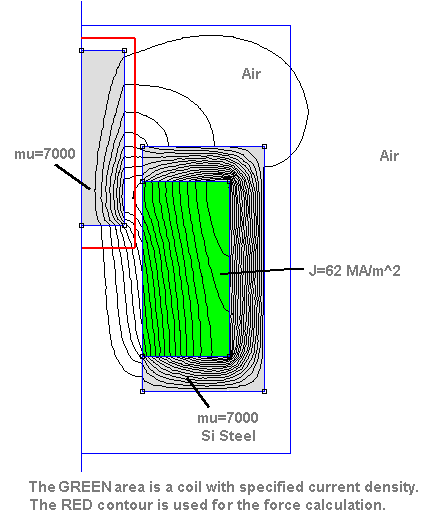
Another feature of FEMM allows us to find a relationship between the coil inductance and the current flowing into it:

Inductance*current^2=integral(A.J dV)

A = Magnetic Potential Vector
J = Current Density

The integration is over the volume of the coil (shown in Green). You don't have to worry about the details of this integration, FEMM takes care of it. With this parameter, we can see the trade-off between the current and the coil inductance. Both of these have to be considered in designing the current switch.

In this particular example, the value of L*I^2 is 3.45 Henry-Amp^2. The total current in the green area is 10,000 amps. If we use 100 turns of wire, the current per turn is 100 amps (10,000/100) and the inductance is 345 microhenries. Eventually we have to deal with the current rise and fall time as determined by the circuit's L/R time constant. If we reduce the current by using more turns of wire, the inductance goes up and so does the L/R time constant, so it takes longer to turn the current on and off.

Conclusion

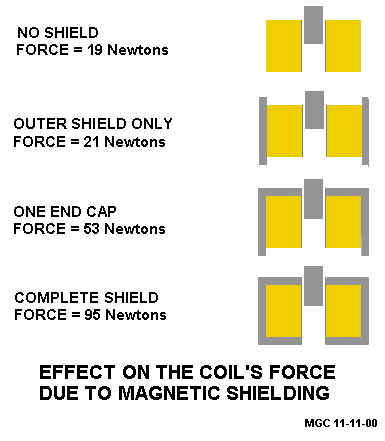As Barry pointed out, a magnetic shield can significantly increase the strength of the field. This figure shows several configurations of shielding. An outer cylinderical shield by itself doesn't significantly increase the force since the flux path in air is still large. Adding one end cap more than doubles the force and caps on both ends nearly double it again.

updated: 11-29-00 MGC