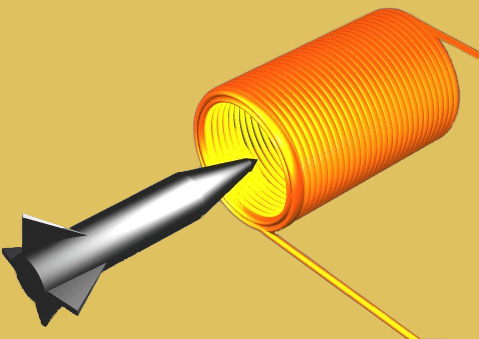
Practical Coilgun Design
FEMM
- Introduction
- Model Setup
- Hollow Cylinder
- Projectile Length
- Inside Diameter
- Iron Washer
- Gun Club
- Coil Current
FEMM - Coilgun Modelling
We can look at a simple particle in a simple wire loop, but what happens with a real object in a long solenoid coil? This requires a Finite Element Analysis program to compute the fields and forces.
I used FEMM to explore the force on projectiles of various lengths. Starting with nearly a particle, I want to explore objects both shorter and longer than the coil itself.
This web page shows how the problem was set up. It includes my FEMM model files so you can explore this yourself. See the next page for my results.
Designing a Generalized Coilgun
I would like to begin with a general-purpose model.
The actual size of the coil is not important, as long as it could be a typical device made by a hobbyist. To keep it simple, we use cylindrical projectiles, assume a some typical iron substance using its B-H curve from FEMM, and neglect eddy currents.
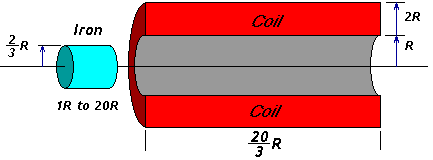 This theoretical coilgun merely represents one possible
model. This is just a starting point. There are an unlimited number of other geometries, many
of which could be superior. But we have to start somewhere!
This theoretical coilgun merely represents one possible
model. This is just a starting point. There are an unlimited number of other geometries, many
of which could be superior. But we have to start somewhere!
Suppose the inner dimension of a coilgun has radius R. Let's express all the other dimensions in terms of R. This model can conceivably be scaled up to send payloads into space, or scaled down to launch BB's or finishing nails.
Notice the gap of 1/3 R between the projectile and the coil. This represents the thickness of the firing tube, and allows a small gap for a loose sliding fit.
Choosing Model Dimensions
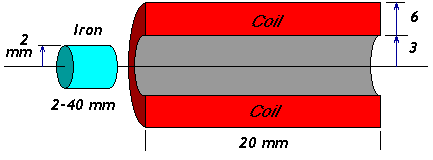 If we choose R = 3 mm, then it is approximately
the same size as the Mark II coilgun.
If we choose R = 3 mm, then it is approximately
the same size as the Mark II coilgun.
As shown at right, this results in a 2mm radius projectile in a 3mm hole down a 6mm diameter coil.
This is a useful start near my preferred projectile size. For example, I've been shooting a 3mm radius iron slug in my Mark 2 coilgun.
Model Definition
I set up this problem in FEMM 3.3, based on the demo2.fem example described by Ian-Stokes Reeves in his tutorial. The positions are measured from the center of the projectile to the center of the coil.
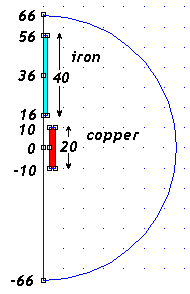 What range of x-positions should we use? The projectile
length will be up to 40mm, and the coil length is 20mm. We need to start the projectile at least
2R (or 6mm) outside the coil. So:
What range of x-positions should we use? The projectile
length will be up to 40mm, and the coil length is 20mm. We need to start the projectile at least
2R (or 6mm) outside the coil. So:
Xmax = (max projectile length)/2 + (coil length)/2 + 2R
Xmax = 20 + 10 + 6 = 36 mm
What range of field should we provide in FEMM? This allows room for the magnetic field to expand
into "free space". I chose to provide 3R (or three times the generalized radius) beyond
the parts. This may be small but the field should be negligible at such distances. Since this
is a semi-circle, the boundary dimension x is:
Xbound = Xmax + (max projectile length)/2 + 3R
Xbound = 36 + 20 + 10 = 66mm
Coil Current in FEMM
How do we choose the current in the copper? Let's pick some typical value, and assume the forces can be scaled up or down accordingly. After all, we are neglecting secondary effects such as saturation and eddy currents. We'll test this assumption later.
The total amp-turns is given by the amperage multiplied by the number of turns. Based on my Mark 2 coilgun, these dimensions can support a four-layer coil with 30 turns per layer, carrying a current of 100 amps.
Let's calculate the total current density for FEMM 3.3. (This becomes much easier in FEMM 4.0 which knows about coils and number of turns, and even computes inductance.)
N*I = (layers)*(turns)*(current) = 4 * 30 * 100 = 12000 amp-turns
This means 12,000 amps would flow in our one-turn equivalent coil in this model. However, FEMM 3.3 needs current density J in mega-amperes per meter-squared, MA/m2. First let's find the cross-sectional area (m2) of this model coil:
Area = (outer radius - inner radius)*(coil length)
Area = (6mm - 3mm)*(20mm) = 60 mm2
Now we know the current and the area. To get current density we divide 12,000 amps by 60 mm-squared, and convert mm-squared to meters-squared:
Current density J = (12000 / 60) * (10002) = 200 mega-amps/meters-squared
What boundary condition should we use? Thankfully the on-line help in FEMM appendix A.3 "Open Boundary Problems" just happens to describe our problem exactly. It describes a solenoidal coil, and suggests using a Mixed Boundary condition at the semicircular radius, with the coefficients:
Coefficient c1 = n/(u0 * r0) = 1 / (4*pi*10-7*0.066)
= 12,057,193
Coefficient c0 = 0
And there you have it! Now refer to Projectile Length page to see how this is scripted for solution.
| < Previous | Page 2 of 8 | Next > |
©1998-2026 Barry Hansen