Critical Damping

Our latest coilgun assumed that a critically-damped system does not suffer from the series damping resistor. But how much energy penalty is in a critically-damped RLC design? Let’s mathematically compare critically-damped to undamped RLC circuits.

The approach is to examine the peak current value in each situation. We’ll analytically find the time t and current I when the current is maximum. Then we’ll compare the two peaks by finding their ratio.

You can skip the messy details and read the surprising conclusion at the bottom of this page.

Critically-Damped Circuit

In general, the current as a function of time for a capacitor discharge is:

(Eqn. 1) where

For a critically-damped RLC circuit this is simplified by using a specific resistance. From this page we know resistance R in critically-damped circuits is:

(Eqn. 2)

Using this value we can simplify α:

(Eqn. 3)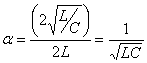

To find the point of maximum current, set the first derivative of I(t)=0 and solve for time t. Let's start by finding the first derivative using the chain rule [f*g]' = f'g + fg':

(Eqn. 4)

Now set this derivative equal to zero and solve for time t:

(Eqn. 5)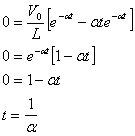

Substitute the known values from equation (1) and (2) above to get the time t of peak current, resulting in the widely accepted value of:

(Eqn. 6)

Now we can find the maximum current peak I_max by inserting this time t into the original equation (1):

(Eqn. 7)

Undamped

An 'undamped' capacitive-discharge is an RLC circuit where resistance R = 0. Although it's not possible to build one, it is very useful because it represents the limiting case of a very high-Q circuit.

The general equation for current as a function of time is:

(Eqn. 8)

The terms α and β are simplified in this manner for an undamped circuit where R = 0:

(Eqn. 9)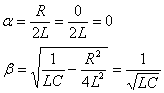

Substitute α and β into the general equation (8) to find I(t) for an undamped circuit:

(Eqn. 10)

Equation (10) above describes an ordinary sine wave. To find the maximum current, we know the first peak occurs at exactly the first quarter of a cycle, or time t = π/2.

Solve for time t at the first peak:

(Eqn. 11)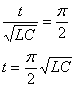

Solve for the maximum current I_max at the first peak, by substituting sin( )=1:

(Eqn. 12)

Comparing Critically-Damped and Undamped Circuits

The equations above have solved for the peak current in both cases. To summarize:

We can compare the results by finding the ratio of peak current from each case:

(Eqn. 13)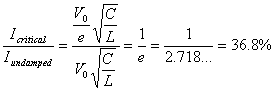

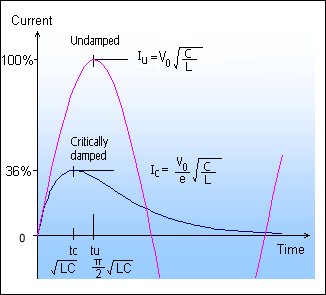
Conclusion

There are two interesting results:

1. A critically-damped RLC circuit will deliver a current peak that is only 36% of the maximum possible peak from an undamped circuit. This is a very heavy penalty for the convenience of a simple circuit!
2. It is somewhat amazing to see a simple result from a complicated analysis. The ratio of 1/e was completely unexpected!