Practical Coilgun Design
Inductors
- Introduction
- Inductive Kickback
- Inductance
- Measure Inductance
- Damped Oscillator
- Critically Damped
Damped Oscillators
An oscillator is anything that has a rythmic periodic response. A damped oscillator has a response that fades away over time. Examples include a swinging pendulum, a bobbing weight on a spring, and also a resistor - inductor - capacitor (RLC) circuit.
The interactive RLC simulation is nice, but what equations drive it? Is there a better approach than a numerical simulation? What component values make it under-damped? Over-damped? When is it a critically-damped oscillator?
Mathemeticians have completely solved the equations that govern a damped oscillator. My web page shows their results, and explains how to compute frequency and critically-damped parts values.
Equations
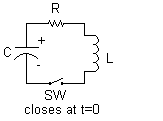 Suppose you have an RLC circuit, which has a resistor + inductor + capacitor in series.
When the switch closes at time t=0 the capacitor will discharge into a series resistor and inductor.
Suppose you have an RLC circuit, which has a resistor + inductor + capacitor in series.
When the switch closes at time t=0 the capacitor will discharge into a series resistor and inductor.
What is the voltage V and current I as a function of time?
Answer:
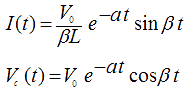
where:
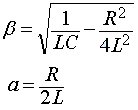
and V= initial voltage
C = capacitance (farads)
R = resistance (ohms)
L = inductance (henrys)
e = base of natural log (2.71828...)
What Does This Mean?
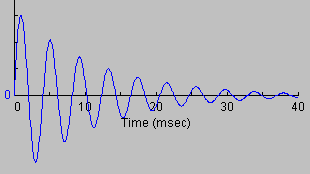
The above equation is the current for a damped sine wave. It represents a sine wave of maximum amplitude (V/BL) multiplied by a damping factor of an exponential decay. The resulting time variation is an oscillation bounded by a decaying envelope.
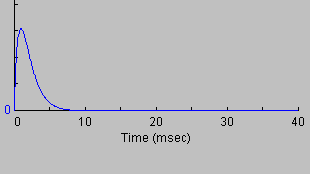
Critical Damping
We can use these equations to discover when the energy dies out smoothly (over-damped) or rings (under-damped).
Look at the term under the square root sign, which can be simplified to: R2C2-4LC
|
 |
|
 |
|
 |
Resonant Frequency
The equations above will tell us the value as a function of time, but what we really want to know is the frequency of oscillation.
An LC circuit will oscillate at an angular frequency of: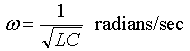
To convert radians/sec to frequency f in Hertz, simply divide by 2p to get this: 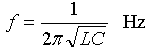
To convert Hz to time period T, use the reciprocal of frequency: ![]()
Examples
Question: What is a coilgun's firing period if it has an RLC circuit where R=0 and C=10,000 µF and L=100 µH?
Answer: The firing period is only the first half-wave of the oscillation.
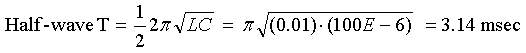
Question: What resistance will make this coilgun critically damped?
Answer: Solve R2C2=4LC for resistance R to get:
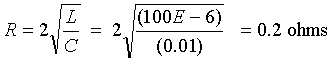
| < Previous | Page 5 of 6 | Next > |
©1998-2026 Barry Hansen