Magnetic Levitation
Levitation
- Introduction
- Why
- Other Maglev
- Hard Drive Maglev
- Schematic
- Parts List
- Buying Parts
- Woodworking
- Other's
- Photographs
- Infrared Emitter
- Photodetector
- Reference Det
- Difference Amp
- Feedback Loop
- Loop Equations
- Bode Plot
- Phase Lead
- Output Amp
- Coil Driver
- PWM
- Lifting Coil
- PSPICE
- Build Time
- PCB
- Power Supplies
- Setup
- Test Power
- Test IR Emitter
- Test Signal Det
- Test Ref Det
- Adjust Sensing Res
- Test Diff Amp
- Test Non-Invert Amp
- Test Coil Driver
- Test Lifting Coil
- Results
Feedback Loop Equations
How does a feedback loop control system really work? Since it appears that every signal depends on every other stage in the loop, how do you compute the overall gain?
We'll continue this discussion of feedback loop stability. First we'll look at the loop equations that describe any such system, and then talk about transfer functions.
This information is really much better explained in "Feedback Loop Stability Analysis" by Walter Friauf, McGraw Hill, (c) 1998, ISBN 0-07-022844.
Loop Equations
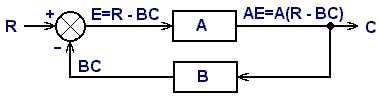 This
diagram shows the basic model for any feedback control system. It shows the four elements in
an abstract manner.
This
diagram shows the basic model for any feedback control system. It shows the four elements in
an abstract manner.
Signal flow is clockwise around the loop. Arrows indicating direction are shown, although they are usually used only at the summing junction, or comparator, which is the circle with the X in it. The inputs (two in this case but there can be any number) have + or - signs to indicate whether each input is added or subtracted. With two inputs and the polarities shown, the summing junction is simply subtracting one signal from the other, in effect performing the comparison that is one of the functions needed for every feedback loop.
The input is labeled R for reference which, in this design, is the ambient light measured by a photodetector in units of volts. The output is C for controlled variable, which is the position measured in millimeters from the center position of the photodetector. The output of the summing junction is E for error signal. Photodetector B converts position into voltage, and the letter B also represents the sensitivity of the detector in units of volts/mm. Block A represents all the stages that process the error signal and drive the lifting coil.
From the equations in the diagram above, we eliminate E, since it is an internal parameter. Solving for the overall gain of the system, we get:
![]()
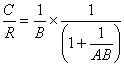
The second form, with 1/B factored out, looks a bit more complicated but is actually more convenient for most purposes, since C/R will be almost exactly 1/B for all useful feedback loops. The reason is that AB will usually be much greater than one, making the other factor in the second form almost unity.
Loop Gain
The overall gain, C/R, is called the closed loop gain since it is the gain from input to output with the loop closed and operating. It is the only gain of any final interest. This gain represents how much the input (reference) signal is amplified at the output.
The real loop gain is the product of all the gains around the loop, AB, and is referred to as the open loop gain. This gain could be measured (theoretically!) by opening the loop anywhere, inserting a small test signal, measuring the signal that appears on the other end of the break, and calculating the ratio.
Despite the simplicity of this equation, it completely describes the behavior of all feedback loop control systems in the world. The transfer functions A and B are arbitrary. These two blocks represent all the signal processing in the forward and reverse directions, and may be fantastically complicated. They may (and usually do!) have frequency-dependent elements and even nonlinear parts. This equation covers them all. The designer's big challenge is to characterize their particular circuit design into these two transfer functions.
Transfer Functions
The characteristics of loop components can be described either by mathematical expressions, called transfer functions, or by graphs. Transfer function is a fancy name for gain.
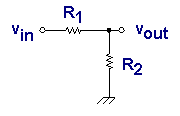 In
the simplest situation the gain of a network or component is just a number that the input is
multiplied by to give the output. For example, a two-resistor voltage divider network. Since
a voltage divider attentuates a signal, instead of amplifying it, the gain is less than unity,
which means that if it is given in decibels, it is negative. This transfer function is Vout/Vin =
R2 / (R1 + R2).
In
the simplest situation the gain of a network or component is just a number that the input is
multiplied by to give the output. For example, a two-resistor voltage divider network. Since
a voltage divider attentuates a signal, instead of amplifying it, the gain is less than unity,
which means that if it is given in decibels, it is negative. This transfer function is Vout/Vin =
R2 / (R1 + R2).
If several components are connected in series, the individual gains are multiplied together to give the overall gain. For example, if two such resistor networks are cascaded together, with buffering to prevent loading effects, the overall gain (attentuation) would be the product of the individual network gains.
For a voltage divider, multiplying the input by the gain will give the output, regardless of the nature of the input. Whether the input is a dc value, sine wave, square wave, or a transient, the output is always the same fraction of the input at every instant. The reason for this simplicity in the case of a voltage divider is that no energy can be stored, so there is no time dependency between the input and output.
When energy storage elements are present, the output at any instant depends on the current value of the input, and also to some degree on previous values. Further, the way previous values affect the output depends on the waveform of the input. For example, the position of the object being lifted depends on its position an instant earlier, along with its previous speed and forces of gravity versus the lifting coil.
| < Previous | Page 16 of 37 | Next > |
©1998-2026 Barry Hansen